指数基金具有成本低、透明度高、长期收益稳定等优点,成为投资者进行“简单投资”的最好选择,而号称“懒人投资法”的基金定投也得到投资者的普遍认可。那么,一个有意思的问题是,如果投资者用最省事的方式进行最简单的投资,其结果会是怎样?
由于指数基金需要锁定跟踪误差,直接以目标指数的市场表现来作为指数基金业绩表现,其代表性强并且简单易懂,因此,本文假定以沪深300指数为跟踪指数,以其正式发布日(即2005年4月8日)为定投起始日期,每月定投一次,按“95%的沪深300收盘指数+5%的现金”的标准,将指数与基期(4月8日收盘指数设定为1元净值)测算出相应的基金净值,进行定投收益模拟。
假设:M为每次定投金额、Pbi是定投申购净值、PSi是定投赎回净值、N是定投次数、Fb是申购费率、FS是赎回费率、R为定投收益率,其公式如下:
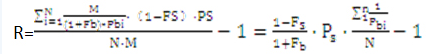
由上述公式可知,定投收益率与基金申购费率、赎回费率、赎回净值、定投申购净值及定投次数(时间)有关,其中,基金申、赎费率由基金公司依据相关规定确定,投资者不能自主确定。投资者可以决定的包括定投次数(包括定投期限和定投频率)、申购净值(由所指定的定投日期确定)和赎回净值,可见,定投日期的选择是影响定投收益的主要原因。准确地进行择时投资是所有投资者“因其不可求而求之”的追求,因此,试图分析不同的定投日期选择所带来的定投收益差异也算是一种投资追求吧。
笔者按以上假设方法对沪深300指数自正式发布日起至2010年9月30日期间,进行按月定投,测算每个日期的1年至4年期的定投收益(因5年期的数据偏少故未测算)。例如,投资者选择每月1号为定投日期,则其1年期定投收益则为连续定投12次后,在第13次定投日期时进行赎回,以此类推,其结果如下表所示(参见附表,申购费率为1%,1年期赎回费率为0.25%):
首先,分析沪深300收盘指数在每月1号-31号的表现情况可以发现,每月5号平均收盘指数最高,对应的每次可得份额最少(按每次定投金额为1000元计);每月18号平均收盘指数最低,对应的每次可得份额最多。那么,是否意味着选择每月18号为定投日期其收益率会最高呢?其实未必,虽然每次可得的定投份额会最多,但由于其赎回时的净值也是平均最低,其结果就取决于两者的平衡结果了。有意思的是,在所考察的四种期限里,每种期限的最低收益率所出现的日期并不完全相同:1年期收益率和4年期最低收益率均出现在每月的10号、2年期最低定投收益率出现在4号,而3年期的则出现在每月的5号,但不同考察期限的最高定投收益率却都出现在每月的14号。从上述公式可以知道,定投收益率是在每次定投申购净值、赎回净值和定投次数间的平衡,在约定定投期限结束后的下一个定投日进行赎回的条件下,最高收益率同时出现在14号应该是一个惊喜。
其次,是否定投的时间越长收益越高?测算的结果显示,从年化收益率(以几何平均值)来看定投时间越长相应的年化收益率并未越高,3年期的定投年化收益率最低,其次为4年期、1年期和2年期,但是随着定投时间越长,其出现最大亏损的值则越小。值得关注的是,2年期定投年化收益率最高,其收益率波动区间最大(最高可达283%,最差的约亏损48%),但出现负收益概率却相对较小。
其三,如果投资者想寻求相同定投次数下积累最多的基金份额,那么选择每月的18号进行定投所得的累积份额将多于每月5日定投所得累积份额的5%,假以时日则差异明显,其中3年期收益率相差(最大)8.8个百分点。此外,四种不同期限的平均最高收益率与最低收益率的差额随着期限的延长而更加显著,依次为1.2%、9.2%、10.2%和13.6%。
最后,“发现规律者消灭了规律”,本文只是对沪深300指数的历史模拟,历史不会简单地重复,或许你可以选择在“18号进行定投申购、在5号进行赎回”,从而获得了超过14号定投的收益,但或许将来未必能如此。
综上所述,每月上、中、下旬收盘指数高于全月均值的比例分别为80%、20%和36%,因此最低收益均出现在上旬,最高收益均出现在中旬;2年期的年化收益率最高,并且其最高定投收益达约283%,而出现负收益概率约为28%。或许省心省力的“懒人投资策略”可以选择在每月中旬进行指数基金定投,定投期限2年左右。(来源: 金融界网站)
附表:不同定投日期不同定投期限的收益率分布
| 日期 | 平均收盘指数 | 对应净值 | 可得份额 | 1年 | 2年 | 3年 | 4年 |
| 1 | 2637.32 | 2.547 | 511.63 | 0.218 | 0.498 | 0.13 | 0.396 |
| 2 | 2652.16 | 2.561 | 513.716 | 0.226 | 0.5 | 0.132 | 0.404 |
| 3 | 2663.80 | 2.572 | 512.445 | 0.226 | 0.502 | 0.134 | 0.41 |
| 4 | 2699.88 | 2.606 | 500.709 | 0.223 | 0.472 | 0.098 | 0.396 |
| 5 | 2701.02 | 2.607 | 500.129 | 0.221 | 0.478 | 0.098 | 0.393 |
| 6 | 2677.79 | 2.585 | 509.443 | 0.224 | 0.5 | 0.13 | 0.399 |
| 7 | 2670.48 | 2.578 | 510.437 | 0.224 | 0.5 | 0.123 | 0.396 |
| 8 | 2619.95 | 2.53 | 524.923 | 0.223 | 0.557 | 0.21 | 0.416 |
| 9 | 2643.80 | 2.553 | 517.452 | 0.225 | 0.532 | 0.163 | 0.407 |
| 10 | 2647.48 | 2.556 | 516.776 | 0.216 | 0.514 | 0.114 | 0.302 |
| 11 | 2619.44 | 2.53 | 524.207 | 0.222 | 0.551 | 0.2 | 0.41 |
| 12 | 2614.08 | 2.525 | 524.882 | 0.223 | 0.552 | 0.195 | 0.411 |
| 13 | 2616.08 | 2.527 | 524.199 | 0.224 | 0.552 | 0.193 | 0.414 |
| 14 | 2640.37 | 2.55 | 523.219 | 0.228 | 0.564 | 0.21 | 0.438 |
| 15 | 2619.53 | 2.53 | 523.727 | 0.221 | 0.543 | 0.19 | 0.403 |
| 16 | 2639.70 | 2.549 | 516.531 | 0.223 | 0.513 | 0.149 | 0.394 |
| 17 | 2636.31 | 2.546 | 516.204 | 0.223 | 0.51 | 0.147 | 0.398 |
| 18 | 2606.49 | 2.518 | 525.515 | 0.227 | 0.546 | 0.186 | 0.427 |
| 19 | 2615.99 | 2.527 | 521.132 | 0.218 | 0.528 | 0.177 | 0.397 |
| 20 | 2625.70 | 2.536 | 519.436 | 0.216 | 0.526 | 0.173 | 0.39 |
| 21 | 2633.33 | 2.543 | 519.4 | 0.219 | 0.532 | 0.172 | 0.389 |
| 22 | 2616.02 | 2.527 | 520.909 | 0.218 | 0.527 | 0.174 | 0.392 |
| 23 | 2642.84 | 2.552 | 513.53 | 0.221 | 0.499 | 0.141 | 0.389 |
| 24 | 2652.24 | 2.561 | 512.109 | 0.222 | 0.499 | 0.137 | 0.389 |
| 25 | 2622.38 | 2.533 | 520.791 | 0.22 | 0.53 | 0.176 | 0.389 |
| 26 | 2616.55 | 2.527 | 522.711 | 0.227 | 0.538 | 0.18 | 0.409 |
| 27 | 2614.46 | 2.525 | 521.701 | 0.222 | 0.531 | 0.169 | 0.385 |
| 28 | 2625.31 | 2.535 | 520.313 | 0.223 | 0.532 | 0.17 | 0.387 |
| 29 | 2618.66 | 2.529 | 520.456 | 0.22 | 0.527 | 0.161 | 0.37 |
| 30 | 2647.81 | 2.557 | 511.909 | 0.219 | 0.491 | 0.121 | 0.366 |
| 31 | 2654.47 | 2.563 | 513.704 | 0.228 | 0.505 | 0.128 | 0.399 |
| 均值 | 2638.433 | 2.548 | 517.234 | 0.222 | 0.521 | 0.157 | 0.396 |
 搜索
搜索